1. 행렬

행렬의 표현

\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
\end{bmatrix}

 

 

• 대괄호 안의 숫자를 성분이라고 한다.
• 성분은 행렬안에 배열된 구성원
• 위와 같은 행렬의 경우 2행 3열 행렬이라고 표현한다.
• aₓᵧ라고 표현할 수 있다.

 

 

용어 정리

주대각선

: 행렬의 왼쪽위에서 대각선 아래를 가르는 선

출처 : 위키백과

 

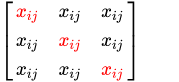
대각행렬

: 대각선에 있는 성분만으로 구성된 행렬(3X3)

 

 

영행렬

: A-A = 0

실수에서 표현하는 0이 아닌, 0으로만 표현된 행렬

출처 : 위키백과

 

전치행렬

: 주대각선을 기준으로 aₓᵧ와 aᵧₓ를 바꾸는 것

 

\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
\end{bmatrix}

 

이 행렬의 전치행렬은 아래와 같다.

 

\begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix}

 

대칭행렬

: 주 대각선을 기준으로 뒤집어도 같게 나오는 행렬

 

 

단위행렬

: 모든 대각성분이 1이고, 그 외 성분은 0인 정사각행렬

\begin{pmatrix} 1 & 0 \\ 0 & 1  \end{pmatrix}

 

\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix}

 

---

행렬의 가감 연산

덧셈, 뺄셈은 각각의 요소끼리 더하고 빼는 것

스칼라를 곱하면 그 요소들 각각에 스칼라를 곱하는 것

 

행렬의 곱셈 연산

• m x n 행렬 A = aₓᵧ와 n x r 행렬 B = bₓᵧ가 있을 때,
• AB = (Cₓᵧ)
• 1행 1열, 1행 2열
• 2행 1열, 2행 2열
• 이렇게 해서 m x r의 행렬이 만들어짐
• 행렬의 곱셈은 교환법칙이 성립하지 않는다.
• 행렬의 곱은 행렬의 합성이라고 봐야 함(합성함수를 만들듯이..)