로드리게스 회전이란?
- 회전 축과 각도가 주어진 공간에서 벡터를 회전시키는 효율적인 알고리즘

- 벡터 v를 방향벡터 a를 중심으로 𝜽만큼 회전시켜서 벡터 v'를 구하는 방법에 대한 내용
- 벡터 v는 수직을 향하는 성분(v ㅗa)과 수평을 향하는 성분(v lla)으로 나눠질 수 있다.

- ①에 해당하는 축의 길이는 vsinα가 된다.
- ①에 해당하는 축을 𝜽만큼 회전시키면 ②가 되는데 각도만 바꾼 것이므로, 크기는 같다.
- 따라서 ②의 크기도 vsinα가 된다.
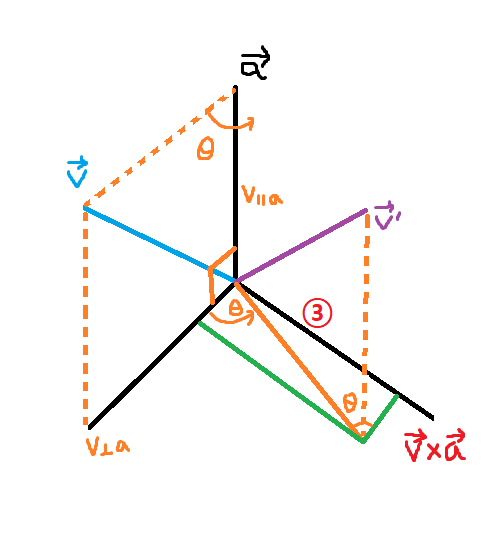
- ③에 해당하는 축은 v와 a의 내적의 결과로 얻을 수 있다.
- 외적의 결과는 v * a * sinα로 구해지는데,
- a는 단위벡터이므로 결과는 vsinα로 위의 ②와 동일한 크기임을 알 수 있다.
결과적으로 v'은 아래와 같은 요소들로 구성되었음을 알 수 있다.
v' = v lla + v ㅗa + (a x v)sinα
이 식을 더 풀어 쓰면
v' = (v · a)a + (v - (v · a)a)cos𝜽 + (a x v)sinα
최종적으로
v' = v cos𝜽 + (v · a)a (1 - cos𝜽) + (a x v)sinα 로 정리된다.
'DirectX > [Inflearn_rookiss] Part2: DirectX12' 카테고리의 다른 글
| 23. Orthographic Projection (0) | 2023.02.02 |
|---|---|
| 22. Quaternion - 개념과 사용 방법 (0) | 2023.02.01 |
| 20. Quaternion - 짐벌락 현상과 복소수에 대한 개념 (2) | 2023.01.30 |
| 19. Frustum Culling (2) | 2023.01.28 |
| 18. SkyBox (0) | 2023.01.27 |




댓글