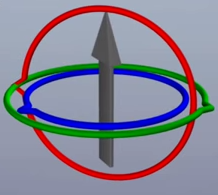
오일러 방식의 문제?
- x축을 90도로 놓고 y축을 회전시키면 z축이 돌아간다. 왜지? 축이 손실된 것
- 이 현상을 짐벌락 현상이라고 한다.
짐벌락 현상이란?
- 각 축의 회전이 결합할 때 세 축 중 하나의 축이 먹통이 되는 현상
- 유니티는 회전을 적용하는 순서가 z - x - y 순으로 적용되는데,
항상 2번째 축에서 문제가 발생한다.
- z축을 회전시키면 x축은 그 영향을 받아 원래 궤도가 아닌 다른 궤도로 움직인다.
이를 해결하기 위해서는?
- 앞으로 배울 쿼터니언의 개념을 도입해야 한다!
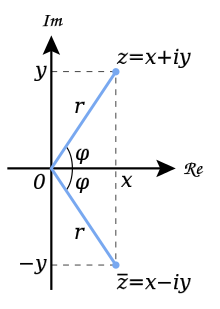
복소수 개념 정리
복소수란?
- a + bi 꼴의 수를 말하며 a는 실수부, bi는 허수부라고 칭한다.
이 수를 벡터와 같이 2차원 평면에 표현할 수 있는데 이 평면을 복소평면이라고 한다.
1) 복소수의 덧셈 뺄셈
-> 실수부는 실수부끼리, 허수부는 허수부끼리 계산할 수 있다.
-> (a + bi) ± (c + di) = (a ± c) + i(b ± d)
2) 복소수의 곱셈
-> 실수의 곱셈과 동일하다
-> (a + bi)(c + di) = ac + adi + bci + bdi²
= (ac - bd) + i(ad + bc)
3) 켤례복소수
-> a + bi의 켤례복소수는 허수부에 -를 붙인 것 (a - bi)
-> 켤례복소수의 성질 : (a + bi)(a - bi)은 a² + b²가 된다.
-> a² + b² + abi - abi = a² + b²
z의 크기를 구해보자!
- z는 우선 a + bi로 나타내므로,
- |z| = |a + bi|가 되고, 피타고라스 정리에 의해 √a² + √b²이 된다는 것을 알 수 있다.
- 또한 위에서 설명했듯 켤례복소수의 곱은 a² + b²이므로, 이는 z의 크기와 연관이 있다는 것을 알 수 있다.
- zz* = (a+bi)(a-bi) = |z|² = a² + b²
다음과 같이 z₁, z₂가 있다고 가정해보자.
z₁ = r₁(cos𝜽₁ + i * sin𝜽₁)
z₂ = r₂(cos𝜽₂ + i * sin𝜽₂)
z₁과 z₂는 위와 같이 이루어져 있을 것이다.
z₁과 z₂를 곱해보면 어떤 결과가 나올까?
전개하면 아래와 같은 식이 된다.
r₁·r₂( (cos𝜽₁·cos𝜽₂) + (cos𝜽₁·i * sin𝜽₂) + (i * sin𝜽₁·cos𝜽₂) + (i * sin𝜽₁·i * sin𝜽₂) )
이 식을 실수끼리, 허수끼리 모으면 아래와 같은 식이 된다.
r₁·r₂( (cos𝜽₁·cos𝜽₂) - (sin𝜽₁·sin𝜽₂) + i( (cos𝜽₁·sin𝜽₂) + (sin𝜽₁·cos𝜽₂) ) )
그런데 이 식을 좀 더 들여다보면 코사인의 합 공식, 싸인의 합 공식으로 간추릴 수 있다.
r₁·r₂( cos(𝜽₁ + 𝜽₂) + i( sin(𝜽₁ + 𝜽₂) ) )
여기서 r₂가 애초에 크기가 1이었다면? 저 식에서 r₂가 날아가게 되고 두 각을 더해준 각도를 구할 수 있게 된다.
결론적으로 복소수 2개를 곱해줬더니 벡터가 회전했다!?
이게 가능한 이유는 i²이 -1이기 때문에 이 식이 성립했기 때문이다!
이 얘기는 복소수의 곱이 회전 행렬과 동일하다는 얘기인데.. 맞나?
- a + bi를 복소평면 상에서 cos𝜽 + i * sin𝜽라고 볼 수 있다.
- 이 식을 각 성분으로 나눠서 행렬로 표현하면
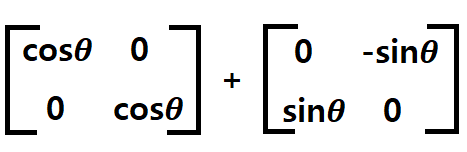
위와 같이 표현할 수 있으며, cos과 sin을 밖으로 빼서 더하면
cos𝜽 * 1+ sin𝜽 * i로 표현될 수 있다.
'DirectX > [Inflearn_rookiss] Part2: DirectX12' 카테고리의 다른 글
| 22. Quaternion - 개념과 사용 방법 (0) | 2023.02.01 |
|---|---|
| 21. Quaternion - 로드리게스 회전 (0) | 2023.01.31 |
| 19. Frustum Culling (2) | 2023.01.28 |
| 18. SkyBox (0) | 2023.01.27 |
| 17. Normal Mapping (0) | 2023.01.27 |




댓글