1. 행렬의 전치연산
위 행렬에서 a와 f를 중심축으로 뒤집는 연산을 전치연산이라고 한다.
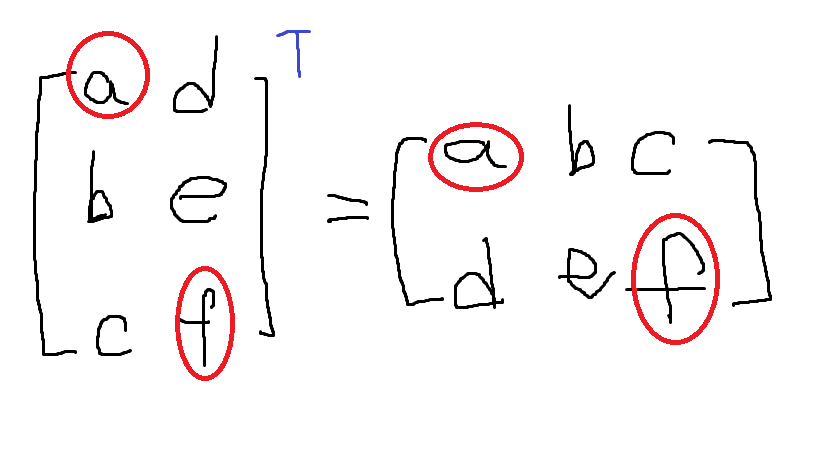
* 정방행렬이란?
전치행렬로 뒤집어도 모습이 같은(성분은 달라지지만 모양은 같음) 행렬
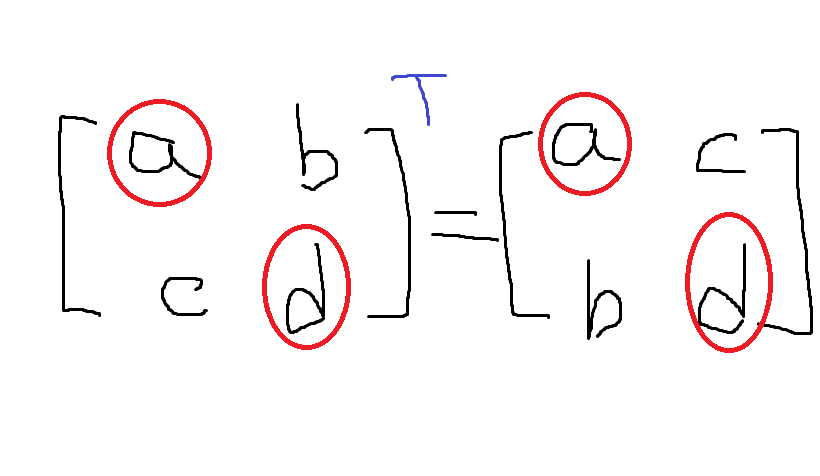
2. 행렬의 곱연산
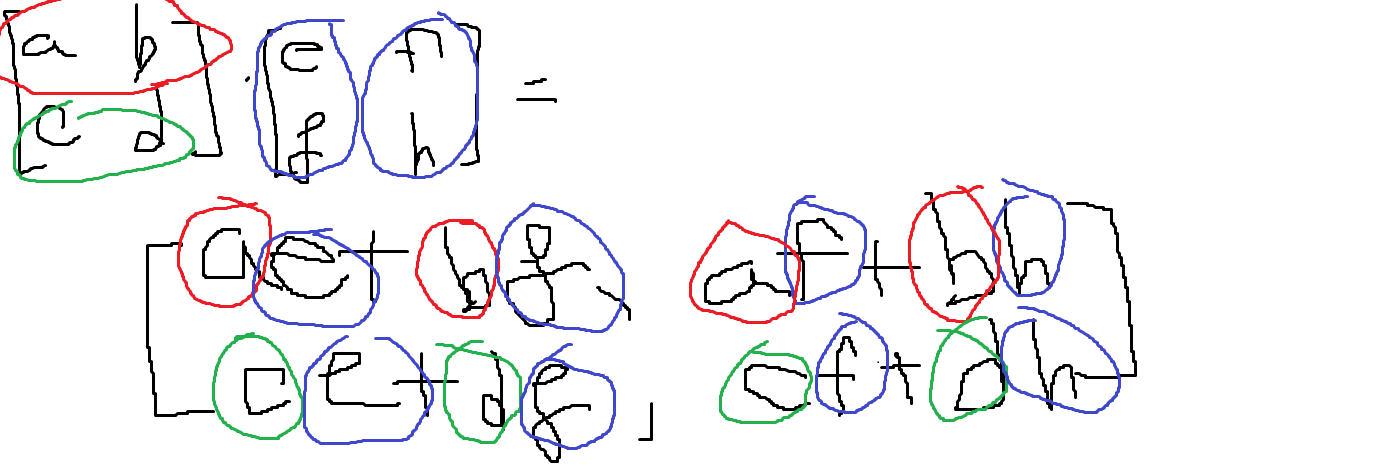
행과 열을 대응시켜 곱하고 그 결과를 더한다
* 행렬은 교환법칙을 만족하지 않고 결합법칙을 만족한다
- A * B != B * A
- A * (B * C) = (A * B) * C
3. 행렬곱의 전치연산
(A * B)^T = B^T * A^T
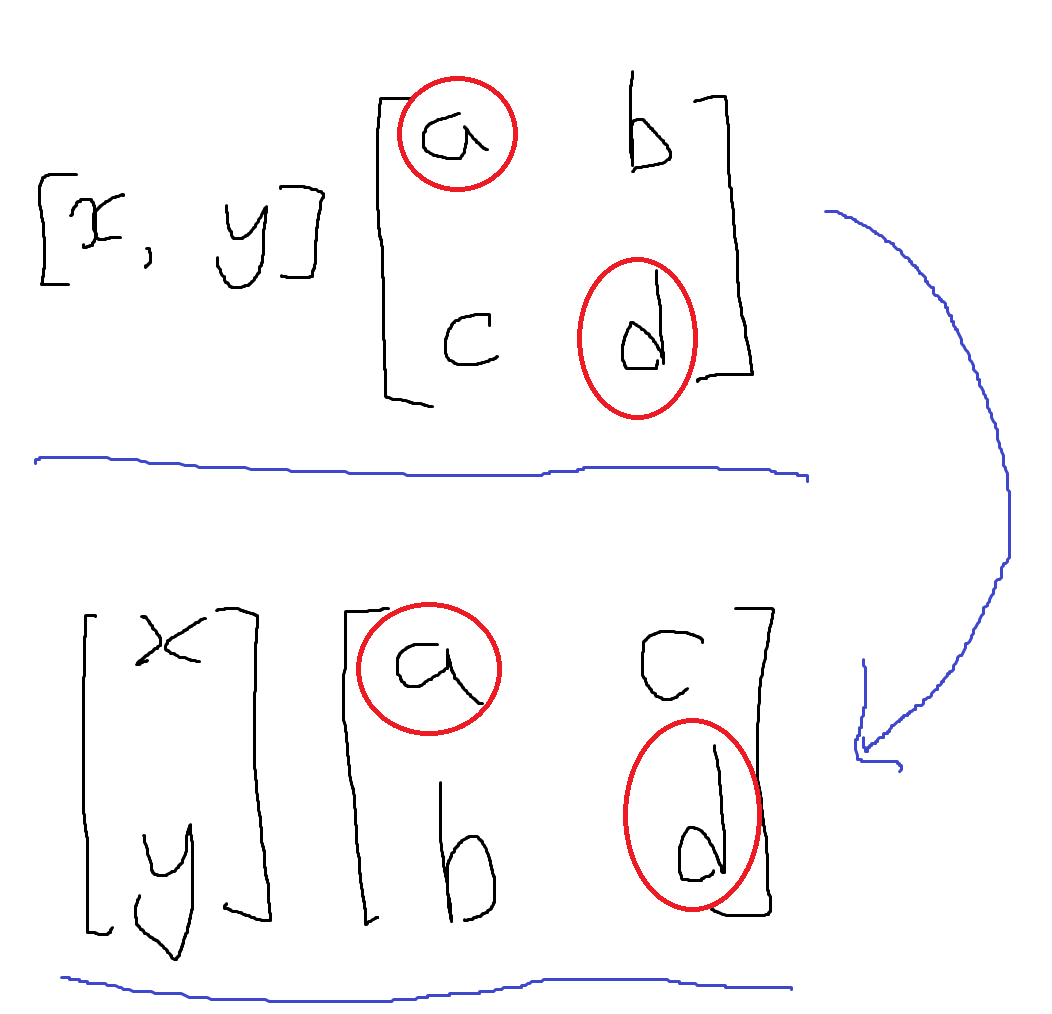
열 기반 행렬과 행 기반 행렬
벡터를 열로 사용하는지 행으로 사용하는지에 따라 열 기반, 행 기반으로 나뉨
또한 열 기반, 행 기반을 어떤 벡터와 2X2 행렬의 곱을 나타낼 때 벡터를 어느 한 상태에서 다른 상태로 변경했을 경우
(EX 열기반 -> 행기반) 2X2행렬은 전치연산이 수행되어야 한다
행렬을 이용한 기저벡터의 변환
표준기저벡터 e1, e2
e1 = (1, 0)
e2 = (0, 1)
임의의 좌표 x,y는 다음과 같이 이루어져 있다.
(x,y) = x(1,0) + y(0,1)
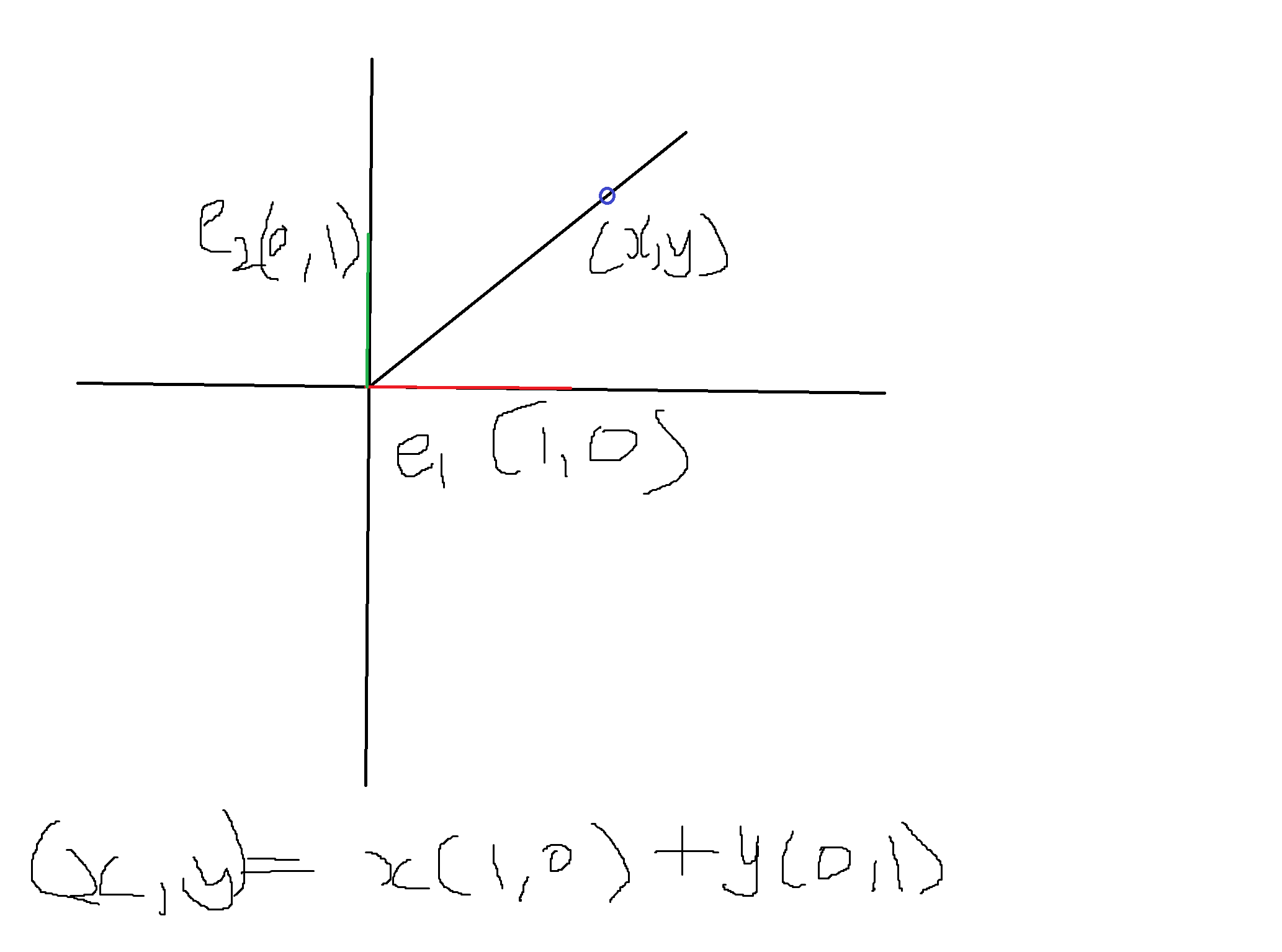
여기서 e1, e2를 행렬을 통해 변환시킬 수 있고 그걸 통해 우리가 원하는 변환을 쉽게 구현할 수 있다.
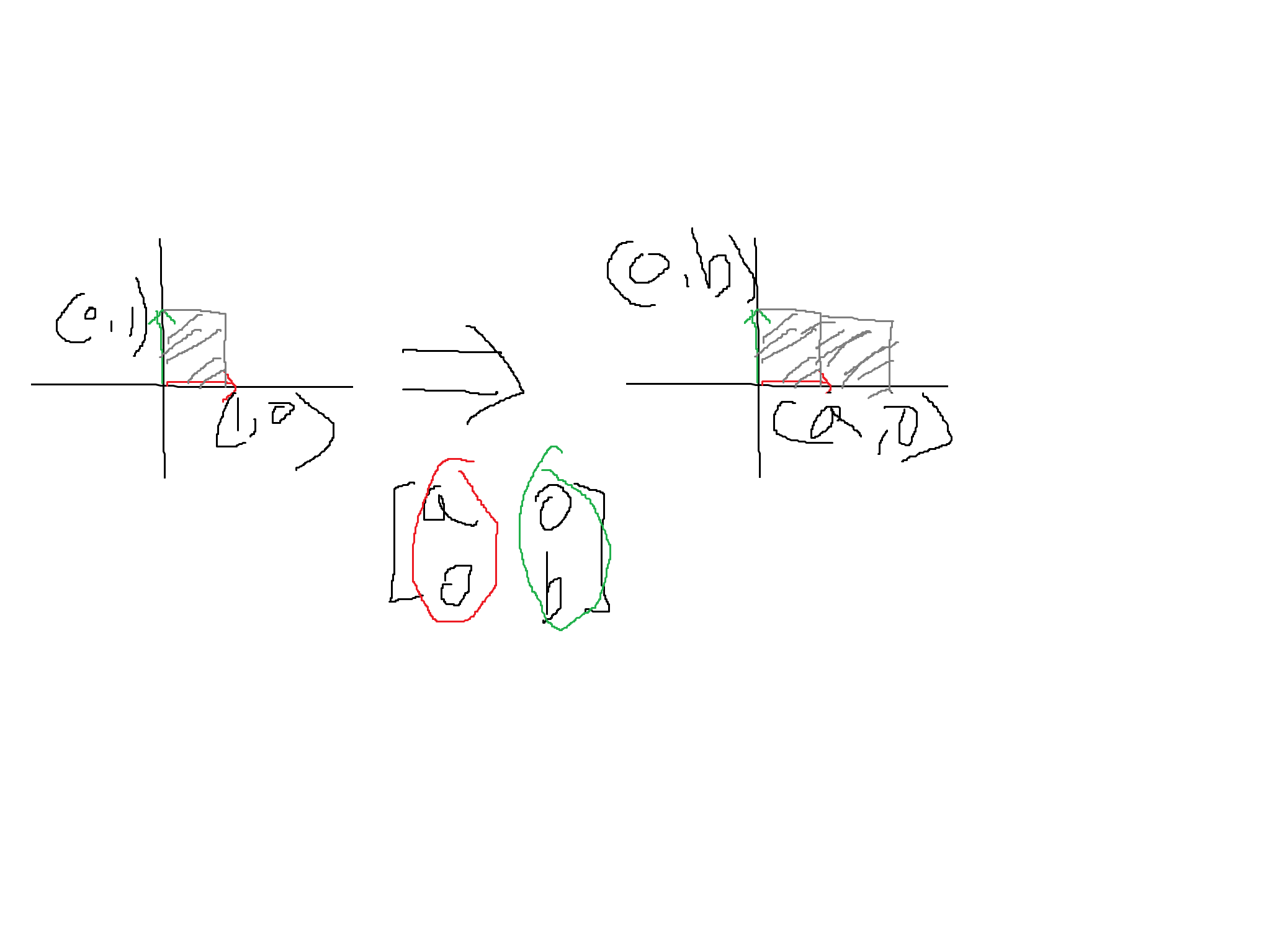
따라서 기저 벡터는 아래와 같이 변환되어서 같은 공간의 다른 벡터들을 한꺼번에 변환시킬 수 있는 것이다.
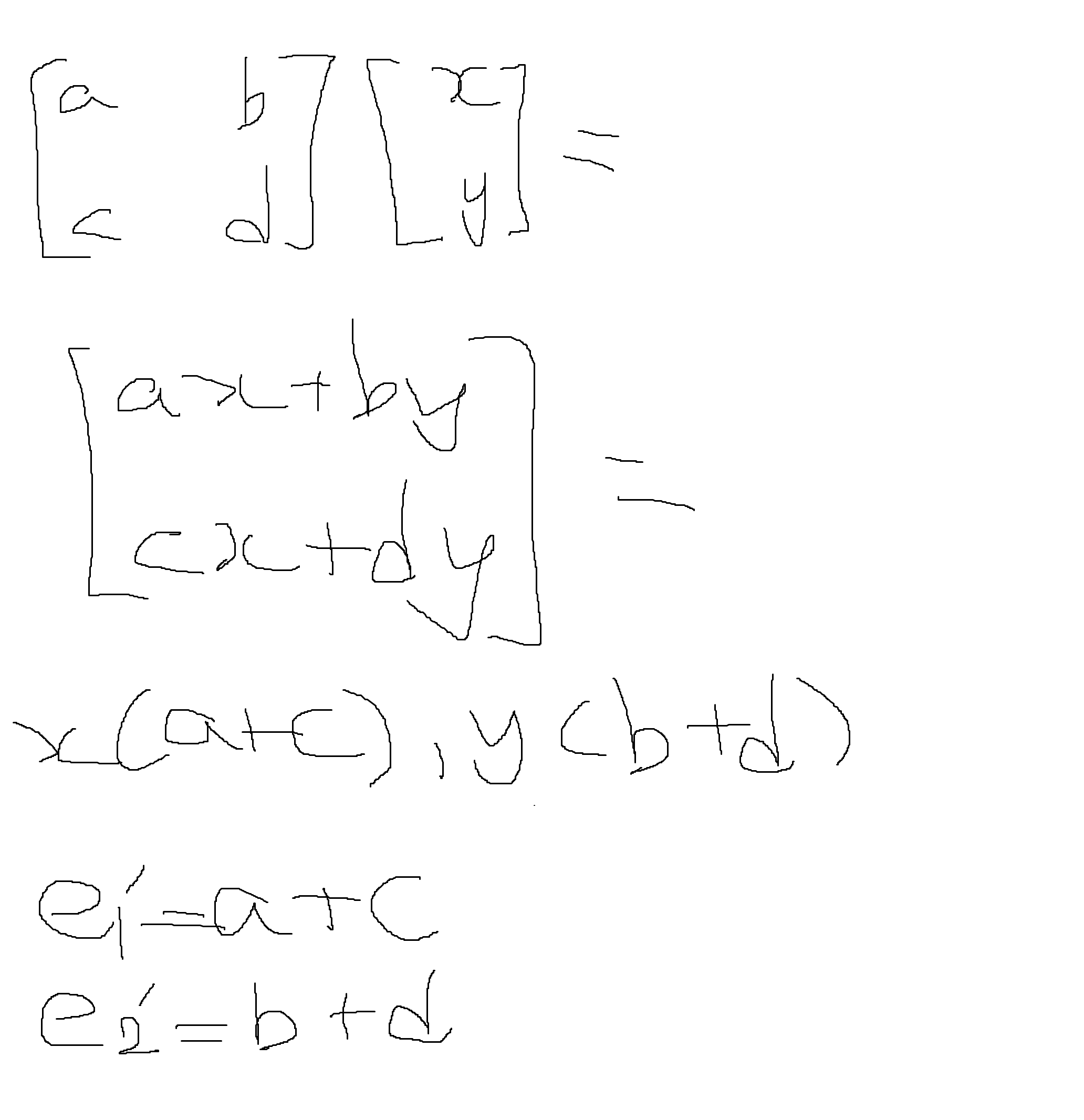
댓글